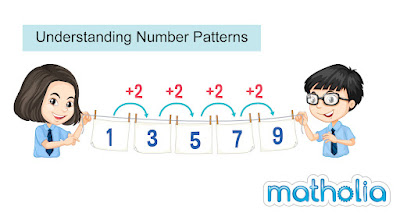
Understanding Number Patterns and How to Avoid Mistakes When Identifying Them
Monday, May 8, 2023
Understanding Number Patterns and How to Avoid Mistakes When Identifying Them
Tuesday, March 21, 2023
Busting the Big Number Myth: How Online Math Learning Can Help Young Learners Understand Number Value
One of the most common misconceptions that young learners encounter in numeracy is the belief that bigger numbers are always greater than smaller numbers. This misconception can arise because young learners often associate larger physical objects with "more" or "greater" than smaller objects. However, when it comes to numbers, this is not always the case. For example, 5 is greater than 3, but 0.3 is actually smaller than 0.5. This misconception can lead to difficulty understanding concepts like place value, fractions, and decimals. To help address this misconception, it is important to teach young learners about number relationships, the value of digits in different places, and how to compare numbers using symbols like greater than and less than.
An online learning math website with lots of instructional videos and dynamic practice, like Matholia, can help remedy the misconception that bigger numbers are always greater than smaller numbers in several ways.
Firstly, instructional videos can provide clear explanations of mathematical concepts that can help to dispel common misconceptions. The videos can explain the relationship between the size of a number and its value, and how this relates to concepts like place value, decimals, and fractions. By presenting information in a clear and accessible way, videos can help young learners to better understand the concepts they are learning.
Secondly, dynamic practice activities can provide opportunities for learners to apply what they have learned in a variety of contexts. For example, learners can practice comparing numbers in different forms, such as written form, numerical form, and visual form. By providing practice opportunities that are varied and engaging, learners can better internalize the concepts they are learning and build their confidence in their abilities.
Thirdly, interactive quizzes and assessments can help learners to identify and address their misconceptions. By providing immediate feedback and guidance, quizzes and assessments can help learners to correct their mistakes and build a deeper understanding of mathematical concepts.
Finally, online learning math websites can provide opportunities for learners to work at their own pace and in their own time. This can be especially helpful for learners who may struggle with math or who have different learning styles. By providing a flexible and supportive learning environment, online learning math websites can help learners to build their confidence and their skills.
An online learning math website with lots of instructional videos and dynamic practice can help remedy the misconception that bigger numbers are always greater than smaller numbers by providing clear explanations, varied practice opportunities, immediate feedback and guidance, and a flexible and supportive learning environment.
Thursday, February 23, 2023
The Bar Model: A Visual Problem-Solving Strategy in Singapore Math that Helps Learners Understand Math Better
The bar model is a visual problem-solving strategy used in Singapore Math that has gained widespread popularity among educators worldwide. It is a powerful tool that helps learners develop a strong conceptual understanding of math concepts by representing problems visually. By using bars or rectangular models to illustrate math problems, learners can break down complex problems into simpler, more manageable parts and make connections between different math topics.
How the Bar Model Works
The bar model is a problem-solving strategy that uses visual models to represent quantities and relationships between them. In a typical bar model, a rectangular bar is used to represent a known or unknown quantity. The bar is then divided into smaller sections, with each section representing a specific part of the quantity. For example, if the bar represents the total number of apples in a basket, then each section could represent the number of apples picked by each person.
The bar model is a versatile tool that can be used to solve a wide range of math problems, from simple addition and subtraction problems to more complex multiplication and division problems. By visualizing the problem, learners can better understand the relationships between different quantities and develop a deeper understanding of the math concepts being taught.
How the Bar Model Helps Learners Understand Math Better
The bar model is an effective tool for helping learners understand math concepts because it enables them to:
Visualize the problem: By representing math problems visually, learners can more easily understand the problem and the relationships between the quantities involved. This can help learners see the problem from different angles and develop a deeper understanding of the math concepts being taught.
Make connections between different math topics: The bar model is a versatile tool that can be used to solve a wide range of math problems. By using the bar model to solve different types of problems, learners can make connections between different math topics and develop a more holistic understanding of math.
Develop critical thinking skills: The bar model encourages learners to break down complex problems into simpler, more manageable parts. This helps learners develop critical thinking skills and improves their ability to solve problems independently.
Build confidence in math: By using the bar model to solve math problems, learners can develop a deeper understanding of math concepts and build confidence in their ability to solve problems.
The bar model is a powerful visual problem-solving strategy that can help learners develop a strong conceptual understanding of math concepts. By representing math problems visually, learners can break down complex problems into simpler, more manageable parts and develop a deeper understanding of the relationships between different quantities. The bar model is a versatile tool that can be used to solve a wide range of math problems, and it encourages learners to develop critical thinking skills and build confidence in math. By incorporating the bar model into math instruction, educators can help learners understand math better and become more effective problem solvers.
Wednesday, February 15, 2023
The Benefits of Adopting Singapore Math for Homeschooling
For many homeschooling parents, teaching math can be a daunting task. Fortunately, there is a well-regarded math curriculum that has gained popularity around the world: Singapore Math. This curriculum is known for its emphasis on problem-solving, visualization, and building a strong foundation in mathematics. In this article, we'll explore some of the benefits of adopting Singapore Math for homeschooling.
Focus on problem-solving: One of the key strengths of Singapore Math is its focus on problem-solving. Students are taught to think critically and approach math problems from multiple angles. This emphasis on problem-solving not only helps students become more proficient in math, but also equips them with valuable skills that they can apply to other subjects and real-world situations.
Strong foundation in mathematics: Singapore Math is known for its strong foundation in mathematics. The curriculum is carefully structured to build a solid understanding of mathematical concepts, starting with the basics and gradually increasing in complexity. This approach helps students develop a deep understanding of math, rather than just memorizing formulas and procedures.
Emphasis on visualization: Another unique feature of Singapore Math is its emphasis on visualization. Students are encouraged to use visual aids, such as bar models and diagrams, to help them understand mathematical concepts. This approach helps students develop a more intuitive understanding of math, making it easier for them to apply what they've learned to new situations.
Clear and concise explanations: Singapore Math textbooks are known for their clear and concise explanations. The curriculum is designed to be easy for students to understand, with concepts introduced in a logical order and explained in a step-by-step manner. This makes it easier for parents to teach math to their children, even if they don't have a strong math background themselves.
Widely recognized and respected: Singapore Math is widely recognized and respected around the world. Many top-performing countries in math, such as Singapore and South Korea, use this curriculum in their schools. This recognition and respect can be a valuable asset for homeschooling parents, who can be confident that their children are receiving a high-quality math education.
Abundance of resources: Finally, there are many resources available for homeschooling parents who wish to adopt Singapore Math. There are numerous textbooks, workbooks, and other materials available for purchase, as well as online resources. Matholia is an online primary mathematics portal based on the latest syllabus from the Ministry of Education, Singapore.The learning portal brings together a wealth of interactive content to ensure that pupils excel in all areas of primary mathematics whilst allowing teachers and parents the opportunity to closely monitor pupils' performance across the syllabus.
In conclusion, Singapore Math is a highly effective math curriculum that is well-suited for homeschooling. Its focus on problem-solving, strong foundation in mathematics, emphasis on visualization, clear and concise explanations, recognition and respect, and abundance of resources make it an ideal choice for homeschooling parents who want to give their children a solid math education.
Sunday, April 19, 2020
Tuesday, March 5, 2019
Problem Solving Task - Baking Cookies
One way to do it is to find the unit value by dividing what we know, the number of Joey’s cookies by the number of units he has: 200 ÷ 5 = 40
The baked 320 cookies altogether.
The Matholia Team
Tuesday, February 26, 2019
The Importance of Problem Solving in Math
Digging deeper into the reasons for Singapore’s success, a pattern emerges. This young country has invested most of its resources in developing a high-quality approach to education. Part of this includes drawing from the best practices from around the world in all subjects. Professionals are sent around the world to study the research and practices in different countries and bring their findings back to the ecosystem of their teacher training.
Another reason for their success is the emphasis on problem solving. Where historically math has been taught at elementary levels as primarily computation practice, Singapore was a leader in changing the focus to problem solving. Not only that, but they took from the work of Jerome Bruner’s The Process of Education (1960) to develop their approach of introducing concepts first through concrete experiences, then pictorially, and then finally the abstract or procedural level. This enables a robust form of learning that supports long-term learning, not only memorization or working memory.